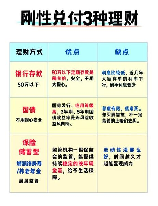
函数的奇偶性详解

在数学分析中，函数的奇偶性是一个非常重要的概念。一个函数的奇偶性描述的是，当自变量取相反数时，函数值是否有变化，即是否对称。对于一个具有奇偶性的函数来说，我们只需要了解在其定义域内的一个区间内即可推出所有值域内的范围。

奇函数和偶函数

一个函数f(x)是奇函数，如果对于其定义域内的任意x有f(-x)=-f(x)。即函数在x轴上对称，函数最中心的点为原点。常见的奇函数有f(x)=x、f(x)=sin(x)。

一个函数f(x)是偶函数，如果对于其定义域内的任意x有f(-x)=f(x)。即函数在y轴上对称，函数最中心的点为y轴。常见的偶函数有f(x)=x²、f(x)=cos(x)。

判断函数的奇偶性

对于一个函数f(x)的奇偶性，有以下几点：

• f(x)为奇函数，当且仅当f(x)=-f(-x)。
• f(x)为偶函数，当且仅当f(x)=f(-x)。
• 如果f(x)既不是奇函数也不是偶函数，则称其为既非奇函数又非偶函数。

函数奇偶性的作用

函数的奇偶性在整个数学分析中具有重要作用。比如在积分计算中，对于奇函数和偶函数的积分计算是有规律的。此外，将函数分解为奇函数和偶函数的组合，可以方便我们求解一些复杂的函数。